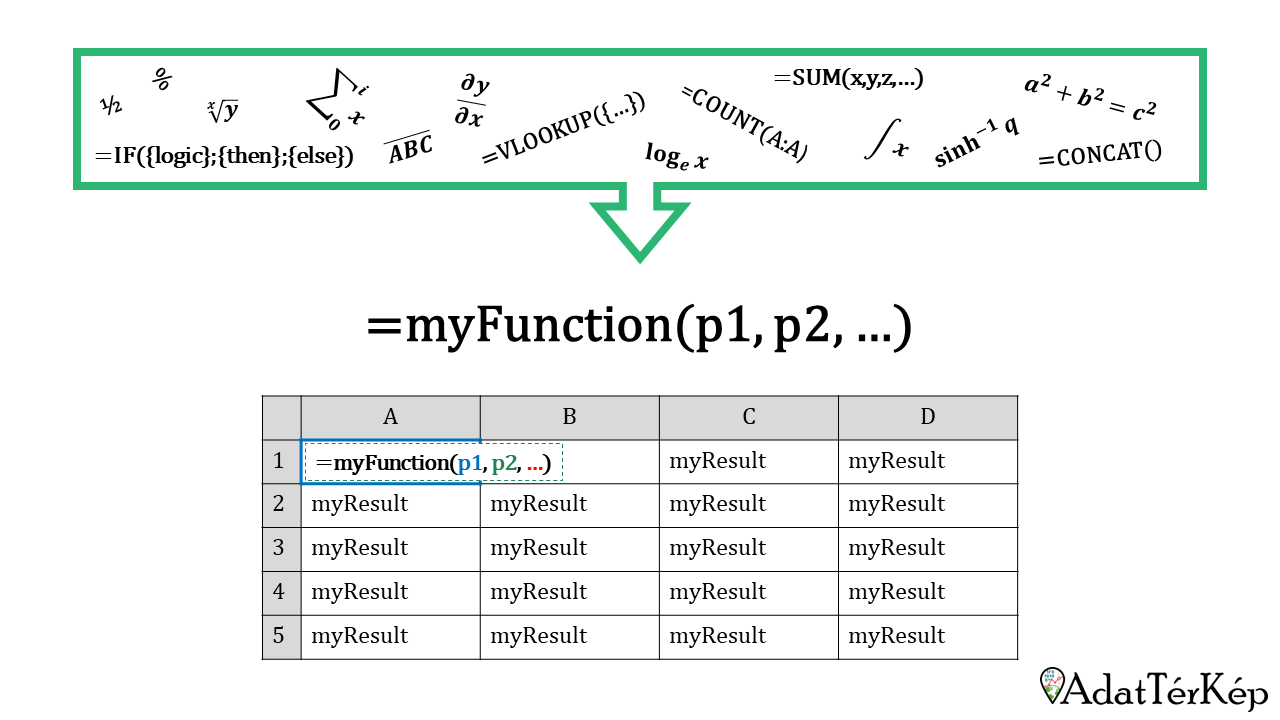
Excel használata során előfordulhatnak olyan összetett, sok függvény együttes használatát igénylő képletek, melyeket időről időre újra meg kell írni (vagy jobb esetben át kell másolni). Milyen jó lenne, ha ezekből a bonyolult logikát megvalósító képletekből valamiképpen egyetlen, könnyen használható függvényt tudnánk készíteni! A jó hír, hogy erre van mód! Egy egyszerű példán keresztül mutatom be, miként lehet saját, egyéni logikánkat megvalósító függvényt létrehozni, amelyet aztán az Excel celláiba írva ugyanúgy tudunk használni, mint például a SZUM() vagy DARAB() függvényeket.
A makróírás alapfogalmait bemutató írásunkban említettük, hogy a makrók két fő típusa különböztethető meg: Sub és Function. A legfontosabb különbség ezek között, hogy az egyik (Sub) csak végrehajtja a belekódolt logikát, a másik (Function) azonban vissza is ad valamilyen értéket, azaz van visszatérési értéke. De vajon hova kerül az az érték, amit a makró visszaad? Ez attól függ, honnan hívtuk meg (használtuk, indítottuk el) a Functiont. Meghívhatja például egy másik makró és a visszatérő értéket eltárolhatja egy változóban. Vagy meghívhatjuk az egyik cellából, ebben az esetben a visszatérő érték az adott cellába kerül. Ha jobban belegondolunk, az utóbbi mechanizmusát követve működnek az Excel saját, jól ismert függvényei is, hiszen amikor egy cellába beírjuk, hogy =SZUM(A2:B4), akkor végrehajtásra kerül a függvény belső logikája (az összegzés) és a visszatérési érték (az összeg) ugyanabban a cellában jelenik meg, ahova a függvényt beírtuk, vagyis ahonnan meghívtuk. Egyéni függvény létrehozásához tehát egy Function típusú makrót kell írnunk, melynek működését mi alakítjuk ki, így azt a feladatot végzi el, ami számunkra fontos.
PÉLDA
Gyakorlati példánk hőse egy egyetemi oktató, aki az egyes kurzusokhoz kapcsolódó feladatok és dolgozatok pontszámait Excelben vezeti. Minden szemeszter végén osztályoznia kell a kurzusok résztvevőinek teljesítményét és minden esetben ugyanazon százalékos eredményesség alapján adja az érdemjegyeket:
- 50% vagy kevesebb: elégtelen
- 50 - 60%: elégséges
- 60 - 70%: közepes
- 70 - 85%: jó
- 85 - 100%: jeles
Bár az arányok mindig azonosak, az egyes kurzusokon különböző számú és pontértékű feladat és dolgozat eredményeképpen lehet pontokat szerezni, így a százalékos eredményesség bázisa kurzusonként más lesz. Nézzünk két kurzust:
- Összesen 100 pont szerezhető 4 házi feladatból (20, 10, 10, 20 pont) és egy dolgozatból (40 pont). (Ezen a kurzuson az a hallgató, aki 61 pontot szerez, 61%-ra teljesít, azaz közepes érdemjegyet kap.)
- Összesen 70 pont szerezhető két dolgozatból (30 és 40 pont). (Ezen a kurzuson az a hallgató, aki 61 pontot szerez, 87%-ra teljesít, vagyis jeles minősítést kap.)
HAGYOMÁNYOS MEGOLDÁS
A pontok rögzítése után hősünk létrehoz egy összegző oszlopot (G oszlop), amelyben összeadja a megszerzett pontokat. Ezután kiszámolja a megszerzett pontok és az összpontszám alapján az értékelés alapját képező százalékot (H oszlop) is. Erre a kerek 100 pontos kurzus esetében igazából nincs szükség, de oktatónk szereti egységes szerkezetben tárolni az adatokat, s száztól eltérő összpontszám esetén szükség van erre az oszlopra is. Végül egy újabb oszlopba (I oszlop) beír egy többszörösen egymásba ágyazott, HA() függvényeket használó képletet, amely a százalékos eredmény alapján meghatározza az osztályzatot:
=+HA(H2<=50,1;1;HA(H2<60;2;HA(H2<70;3;HA(H2<85;4;5))))
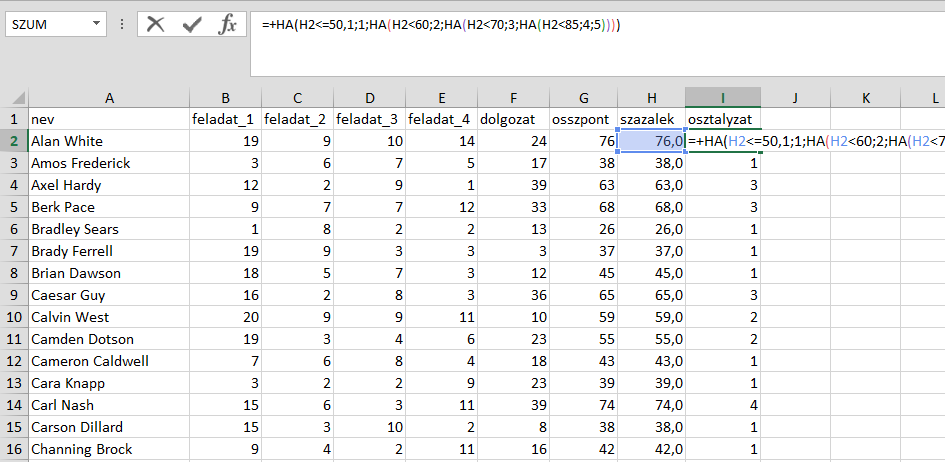
Mivel hősünk kellően leleményes, a képletet átmásolja a második kurzushoz úgy, hogy az ottani százalékra hivatkozzon.
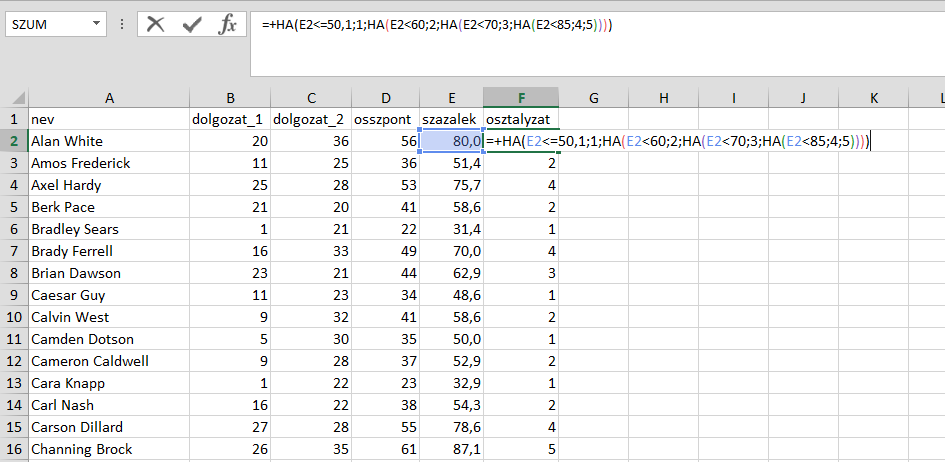
MEGOLDÁS EGYÉNI FÜGGVÉNY HASZNÁLATÁVAL
A fenti megoldás tökéletes a feladathoz. Azonban több szemeszteren keresztül, szemeszterenként több kurzus esetén újra és újra megírni vagy a korábban használtat előkeresni körülményes. Ezért hatékonyabb lehet ugyanezt a logikát átültetni egy makróba, ez esetben egy Functionbe.
Először a Function és End Function kulcsszavak segítségével létrehozzuk a kód kereteit. Adunk neki egy nevet is, pl. giveMarks. Írunk komment formájában egy rövid magyarázatot is, hogy később könnyebben tudjuk értelmezni saját kódunkat.
Function giveMarks()
'A makró célja, hogy létrehozzon egy olyan függvényt, amely segítségével az összpontszám'
'kijelölésével, valamint a maximális pontszám megadásával meghatározható az érdemjegy.'
End Function
Következő lépésben megadjuk a függvény bemeneti paramétereit. Az egyik egy tartomány (Range) típusú objektum lesz, amire az rng karaktersorozattal hivatkozunk majd a makró belső logikájának felépítésekor. A másik egy szám típusú objektum (maxPoints), amely a kurzuson szerezhető maximális pontszámot jelenti majd. Így megspórolható a százalék kiszámítása: elvégzi helyettünk a makró.
Function giveMarks(rng As Range, maxPoints As Integer)
'A makró célja, hogy létrehozzon egy olyan függvényt, amely segítségével az összpontszám'
'kijelölésével, valamint a maximális pontszám megadásával meghatározható az érdemjegy.'
End Function
A tartomány (Range) típus egynél több cellát is tartalmazhat, nekünk azonban fontos, hogy csak egy cella legyen kijelölve. Ezért beépítünk egy ellenőrzést a makróba, amely ellenőrzi, hogy a megadott tartomány hány cellából áll, s ha egynél többől, akkor leállítja a Functiont. Ez az ellenőrzés nem kötelező, pusztán egy biztonsági intézkedés. Ha bízunk magunkban (illetve bárki más, jövőbeni felhasználóban), hogy mindig csak egy cellát jelölünk ki, akkor ez a lépés elhagyható.
Function giveMarks(rng As Range, maxPoints As Integer)
'A makró célja, hogy létrehozzon egy olyan függvényt, amely segítségével az összpontszám'
'kijelölésével, valamint a maximális pontszám megadásával meghatározható az érdemjegy.'
'Ellenőrizzük, hogy valóban csak egy cellát jelölt-e ki a függvény hívása során.'
If rng.Cells.Count > 1 Then
'Ha nem, hibaüzenetet írunk ki és kilépünk.'
giveMarks = "Csak egy cellát jelölj ki!"
Exit Function
End If
End Function
És végül, de nem utolsó sorban írjuk bele azt az összetett döntési logikát, amely a képletben is megjelenik. Egy többágú If-Then-ElseIf-Else döntési fát kell írnunk ehhez, amelybe számszerűen "beleégetjük" az érdemjegyek százalékos határait. (Ez nem mindig bölcs döntés, többnyire próbáljuk kerülni az ilyen "hard coded" megoldásokat.)
Function giveMarks(rng As Range, maxPoints As Integer)
'A makró célja, hogy létrehozzon egy olyan függvényt, amely segítségével az összpontszám'
'kijelölésével, valamint a maximális pontszám megadásával meghatározható az érdemjegy.'
'Ellenőrizzük, hogy valóban csak egy cellát jelölt-e ki a függvény hívása során.'
If rng.Cells.Count > 1 Then
'Ha nem, hibaüzenetet írunk ki és kilépünk.'
giveMarks = "Csak egy cellát jelölj ki!"
Exit Function
End If
'A megszerzett pontszám (rng.Value) és a maximális pontszám (maxPoints) alapján százalékot'
'számolunk, amely alapján meghatározzuk az érdemjegyet.'
If (rng.Value / maxPoints * 100) <= 50 Then
giveMarks = 1
ElseIf (rng.Value / maxPoints * 100) < 60 Then
giveMarks = 2
ElseIf (rng.Value / maxPoints * 100) < 70 Then
giveMarks = 3
ElseIf (rng.Value / maxPoints * 100) < 85 Then
giveMarks = 4
Else
giveMarks = 5
End If
End Function
Készen is vagyunk. Megnyitva az előbbi Excel fájlt, egy újabb oszlopba elkezdjük begépelni a =giveMarks() függvény nevét, majd megadjuk a szükséges paramétereket (cella és max. pontszám). Az egyéni függvény pedig ugyanúgy fog viselkedni, mint bármelyik másik, így például lehúzhatjuk és automatikusan kitölti a többi cellára is.
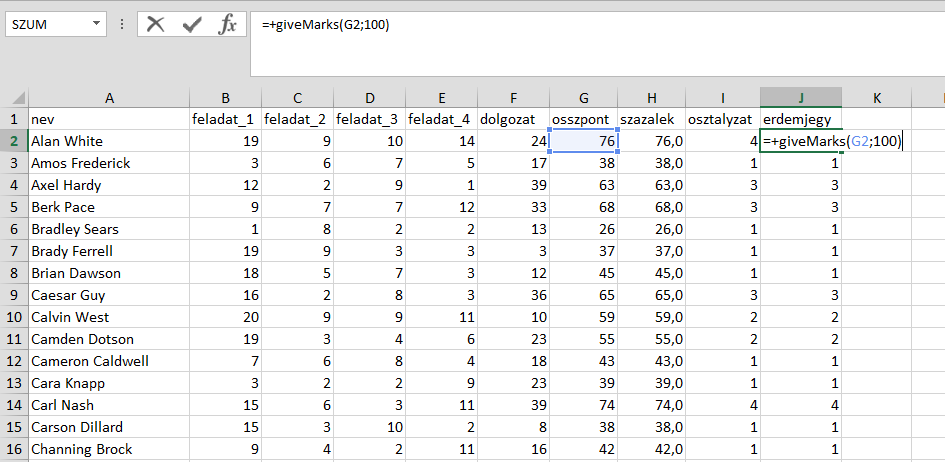
A maximális pontszám paraméterként való átadásának köszönhetően elég az összpontszám oszlop (osszpont), a százalékos eredmények oszlopára már nincs szükség. A képlet pedig könnyen másolható és módosítható, így a második kurzus jegyeit is gyorsan kiszámíttathatjuk.
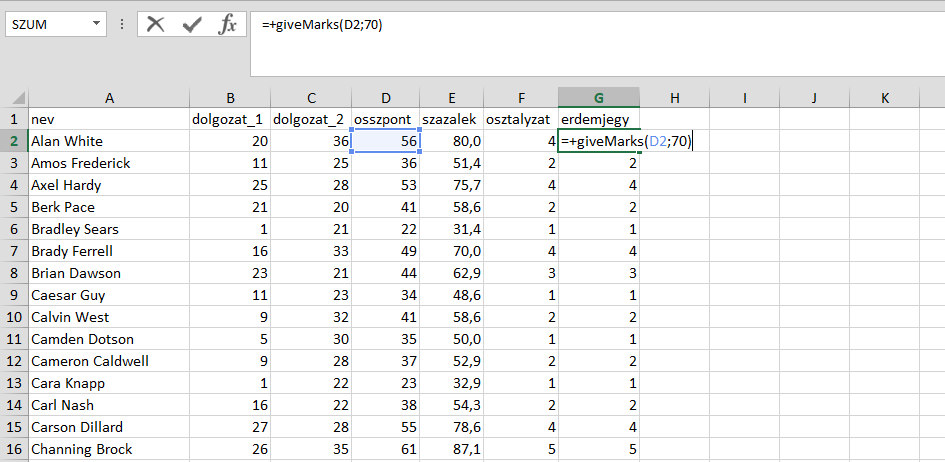
A makrót megtalálod GitHub oldalunkon is!